How To Help Students Learn Properties Of Quadrilaterals

What are the Properties of Circadian Quadrilaterals?

Cyclic quadrilateral

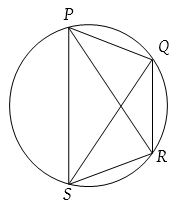
If all four points of a quadrilateral are on circumvolve and so it is called cyclic Quadrilateral.
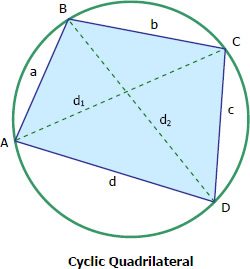A quadrilateral PQRS is said to be circadian quadrilateral if there exists a circle passing through all its four vertices P, Q, R and S.
Let a circadian quadrilateral exist such that
PQ = a, QR = b, RS = c and SP = d.
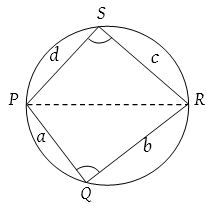And so ∠Q + ∠S = 180°, ∠A + ∠C = 180°
Let  2s = a + b + c + d

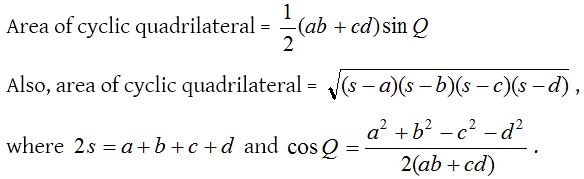
(one) Circumradius of cyclic quadrilateral: Circum circle of quadrilateral PQRS is also the circumcircle of ∆PQR.

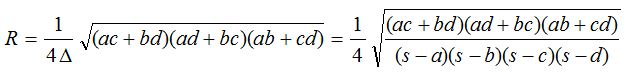
(2) Ptolemy's theorem: In a circadian quadrilateral PQRS, the product of diagonals is equal to the sum of the products of the length of the contrary sides i.e., According to Ptolemy'south theorem, for a circadian quadrilateral PQRS.
PR.QS = PQ.RS + RQ.PS.

Properties of Circadian Quadrilaterals

Theorem: Sum of opposite angles is 180º (or opposite angles of cyclic quadrilateral is supplementary)

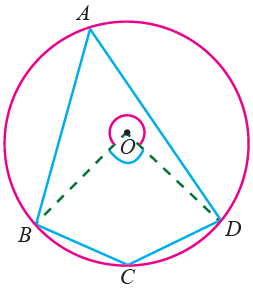
Given : O is the centre of circumvolve. ABCD is the circadian quadrilateral.
To testify : ∠BAD + ∠BCD = 180°, ∠ABC + ∠ADC = 180°
Construction : Join OB and OD
Proof:
(i) ∠BAD = (\(\frac { one }{ 2 } \))∠BOD.
(The angle substended by an arc at the middle is double the angle on the circumvolve.)
(two) ∠BCD = (\(\frac { i }{ 2 } \)) reflex ∠BOD.
(three) ∠BAD + ∠BCD = (\(\frac { one }{ 2 } \))∠BOD + (\(\frac { 1 }{ 2 } \)) reflex ∠BOD.
Add together (i) and (ii).
∠BAD + ∠BCD = (\(\frac { 1 }{ 2 } \))(∠BOD + reflex ∠BOD)
∠BAD + ∠BCD = (\(\frac { ane }{ 2 } \)) × (360°)
(Complete angle at the middle is 360°)
∠BAD + ∠BCD = 180°
(iv) Similarly ∠ABC + ∠ADC = 180°.

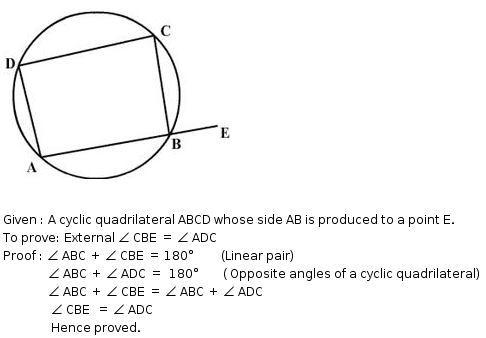
Exterior angle: Exterior angle of cyclic quadrilateral  is equal to reverse interior bending.

Read More:

• Different Kinds of Quadrilateral
• More Solved examples on Quadrilaterals
• RS Aggarwal Class 9 Solutions Quadrilaterals and Parallelograms

Properties of Cyclic Quadrilaterals Instance Bug With Solutions

Instance i:Prove that the quadrilateral formed by the internal angle bisectors of whatsoever quadrilateral is cyclic.
Solution:

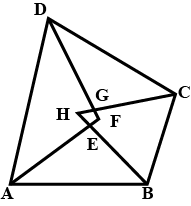
Given a quadrilateral ABCD with internal bending bisectors AF, BH, CH and DF of angles A, B, C and D respectively and the points E, F, G and H course a quadrilateral EFGH.
To prove that EFGH is a cyclic quadrilateral.
∠HEF = ∠AEB [Vertically opposite angles] ——– (one)
Consider triangle AEB,
∠AEB + \(\frac { 1 }{ 2 } \) ∠A + \(\frac { 1 }{ ii } \) ∠ B = 180°
∠AEB = 180° – \(\frac { i }{ two } \) (∠A + ∠ B) ——– (two)
From (one) and (2),
∠HEF = 180° – \(\frac { 1 }{ 2 } \) (∠A + ∠ B) ——— (3)
Similarly, ∠HGF = 180° – \(\frac { one }{ two } \) (∠C + ∠ D) ——– (4)
From iii and 4,
∠HEF + ∠HGF = 360° – \(\frac { 1 }{ 2 } \) (∠A + ∠B + ∠C + ∠ D)
= 360° – \(\frac { 1 }{ 2 } \) (360°)
= 360° – 180°
= 180°
Then, EFGH is a circadian quadrilateral since the sum of the opposite angles of the quadrilateral is 180°

Example 2:ABCD is a circadian quadrilateral whose diagonals intersect at a signal E. If ∠DBC = 70º, ∠BAC is 30º, Detect ∠BCD. Farther, if AB = BC, find ∠ECD.
Solution:

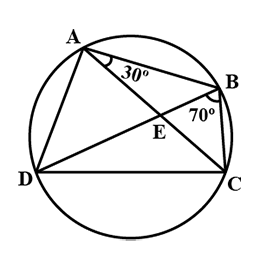
For chord CD,
∠CBD = ∠CAD … Angles in same segment
∠CAD = 70°
∠BAD = ∠BAC + ∠CAD = 30° + 70° = 100°
∠BCD + ∠BAD = 180° …Opposite angles of a cyclic quadrilateral
⇒ ∠BCD + 100° = 180°
⇒ ∠BCD = 80°
In △ABC
AB = BC (given)
∠BCA = ∠CAB … Angles contrary to equal sides of a triangle
∠BCA = thirty°
Also, ∠BCD = 80°
∠BCA + ∠ACD = eighty°
⇒ thirty° + ∠ACD = 80°
∠ACD = 50°
∠ECD = fifty°

Case 3:Testify that a cyclic parallelogram is a rectangle.
Solution:

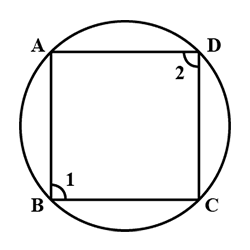
Given that, ABCD is a cyclic parallelogram.
To prove, ABCD is a rectangle.
Proof:
∠ane + ∠2 = 180° …Opposite angles of a cyclic parallelogram
Likewise, Reverse angles of a cyclic parallelogram are equal.
Thus,
∠1 = ∠ii
⇒ ∠1 + ∠1 = 180°
⇒ ∠1 = 90°
I of the interior bending of the parallelogram is right angled. Thus, ABCD is a rectangle.

Source: https://www.aplustopper.com/properties-of-cyclic-quadrilaterals/

Posted by: hanselldientiong.blogspot.com

Share this post